 ОГЛАВЛЕHИЕ
ОГЛАВЛЕHИЕ
 >>>
>>>
Понятие энтропии было введено Р. Клаузиусом, сформулировавшим второе начало термодинамики, согласно которому переход теплоты от более холодного тела к более теплому не может происходить без затраты внешней работы.
Позднее Р. Больцман дал статистическую трактовку энтропии через вероятность нахождения молекул идеального газа в некоторой фиксированной ячейке фазового пространства. В этой трактовке, ставшей для нас привычной, понятие энтропии играет существенную роль как своеобразная мера упорядоченности физической системы.
Сам факт, что изучение порядка оказывается возможным в терминах случайных событий, весьма любопытен с методологической точки зрения. В самом деле, с понятием порядка, упорядоченности связывают обычно наличие строгой закономерности в расположении элементов системы, жесткой детерминации отношений и связей между ними. Порядок исключает хаос. Но вот оказывается, что упорядоченность можно оценить и измерить лишь при условии, что система будет описываться как статистический объект, в котором допускаются хаос и неразбериха. Другими словами, порядок предполагает хаос.
Глубокая связь между понятиями порядка и хаоса, организации и дезорганизации послужила сильнейшим стимулом к проведению целого ряда серьезных исследований понятия энтропии и ее роли как в области физических явлений, так и в мире живой природы.
Энтропия характеризует определенную направленность процесса в замкнутой системе. В соответствии со вторым началом термодинамики возрастанию энтропии соответствует направление теплового потока от более горячего тела к менее горячему. Непрерывное возрастание энтропии в замкнутой системе происходит до тех пор, пока температура не выровняется по всему объему системы. Наступает, как говорят, термодинамическое равновесие системы, при котором исчезают направленные тепловые потоки и система становится однородной.
Абсолютное значение энтропии зависит от целого ряда физических параметров. При фиксированном объеме энтропия увеличивается с увеличением температуры системы, а при фиксированной температуре увеличивается с увеличением объема и уменьшением давления. Нагревание системы сопровождается фазовыми превращениями и снижением степени упорядоченности системы, поскольку твердое тело переходит в жидкость, а жидкость превращается в газ. При охлаждении вещества происходит обратный процесс, упорядоченность системы возрастает. Эта упорядоченность проявляется в том, что молекулы вещества занимают все более определенное положение относительно друг друга. В твердом теле их положение фиксировано структурой кристаллической решетки (с точностью до колебательного процесса, интенсивность которого зависит от температуры тела).
Следует подчеркнуть, что формальное определение энтропии само по себе не опирается на субстанциональные характеристики систем. Другими словами, вовсе не важно, из чего построена система. Зато важно, как она себя ведет: является ли ее поведение детерминированным, однозначно определенным или существенную роль играют случайные процессы. Легко поэтому понять, почему энтропия оказывается важной категорией также за пределами физики, в отраслях науки, где изучаются вероятностные процессы, в том числе в теории информации.
Математическая теория информации ведет свое летосчисление от работ Н. Винера и К. Шеннона, появившихся в конце 50-х гг. Теория была построена на базе статистических методов. Понятие энтропии играет в ней центральную роль как мера информации, точнее, как мера неопределенности. Снятие неопределенности (уничтожение энтропии) трактуется как акт получения информации. Где появляется информация, там исчезает энтропия.
Предположим, мы наблюдаем поведение некоторой системы и нам известно, что в следующий момент (скажем, через 1 мин) система может оказаться в одном из N состояний с вероятностями соответственно р1, p2,..., PN, причем
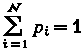
Обычное определение энтропии для этого случая:
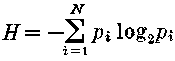
Из данного примера видно, что энтропия характеризует как бы меру неопределенности будущего события, будущего поведения системы. С этой точки зрения упорядоченность любой системы может трактоваться как мера предсказуемости ее будущего. Данная мысль проводится в работе В. В. Дружинина и Д. С. Конторова [1].
Таким образом, говоря об энтропии, мы неявно определяем (и количественно измеряем) отношение системы к самой себе, взятой в другой момент (или другие моменты) времени. Энтропия выступает здесь как поведенческая характеристика системы, определенным образом взаимодействующей с наблюдателем. Полученная ситуация в известной степени сходна с той, которая возникает в квантовой механике, где истолкование вероятностного поведения микрочастиц связывается с особенностями макроскопических средств наблюдения/Аналогия усиливается если принять во внимание, что акт получения информации по своей природе дискретен и сводится к регистрации событий в терминах "да-нет". При получении информации энтропия исчезает скачком, напоминая акт мгновенного сжатия (редукция) волновой функции при попадании микрочастицы на регистрирующую фотопластинку. Не будем настаивать на том, что данная аналогия позволяет свести квантовомеханические процессы к информационным. Такое сведение было бы скорее всего неправильным. Во всяком случае, ясно одно: информационные процессы, как и квантовомеханические, имеют функциональную природу и должны рассматриваться прежде всего с позиции функционального подхода.
Продолжим обсуждение примера, где рассматривалась система с N состояниями. Предположим теперь, что вероятности р1, p2,..., pN характеризуют поведение системы в любой момент времени. Это могут быть, например, предельные вероятности марковской цепи, достигшей равновесия. Предполагается, что над системой не проводится актов наблюдения. Но если такой акт проведен, то марковская цепь возвращается к исходному состоянию и вновь приходит к равновесию лишь по истечении достаточно большого количества времени. В течение этого времени ее энтропия возрастает от нулевого значения до максимальной величины Н, определяемой предельными вероятностями. В равновесии система ведет себя так, что с вероятностью pi пребывает в i-м состоянии. Образно выражаясь, она проводит в i-м состоянии pi-ю часть своего времени. Мы говорим, что Η; характеризует меру упорядоченности системы. Если бы все свое время система проводила в одном состоянии, то соблюдалось бы Η = 0, независимо от того, в каком из N состояний она фактически находилась.
В качестве меры упорядоченности системы удобно использовать введенную Шенноном величину "избыточности" [2]:
R = 1 – H/Hmax
При Η = 0 получаем R = 1. Если все состояния системы одинаково предпочтительны, т.е. р1 = р2 = ... = PN = 1/N, то R = 0 (минимальная упорядоченность).
В целях более наглядного представления энтропию можно рассматривать как измеренное в логарифмической шкале число предпочтительных состояний системы, т.е. совокупность состояний, в которых система пребывает подавляющую часть своего времени. Определим это число формулой n – 2Н. Число предпочтительных состояний n равно 1, если система проводит все свое время в одном состоянии (H = 0). При H = Hmax = log2N все состояния системы одинаково предпочтительны и n = N.
С упорядоченностью системы нередко связывают (или даже отождествляют) понятие организованности. Некоторые авторы [3] используют для оценки степени организованности шенноновскую "избыточность" R. В одной из работ [4] введены даже три критерия. Наряду с критерием R, который авторы называют мерой относительной организованности, вводится также критерий абсолютной организованности системы, определяемый величиной Rабс = RHmax Третий критерий dH/dt вводится для оценки направления и скорости организационной эволюции системы. Следуя за Г. Ферстером [5], авторы делят системы (в соответствии со значением третьего критерия) на термодинамические (dH/dt > 0), механические (dH/dt = 0) и самоорганизующиеся (dH/dt < 0).
Если использовать формулу для числа предпочтительных состояний, то легко показать, что упомянутый выше критерий абсолютной организованности Rабс определяет долю предпочтительных состояний относительно максимально возможного их числа:
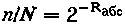
Увеличение абсолютной организованности ведет к резкому уменьшению доли состояний, в которых фактически пребывает система. Так, стремясь повысить свою организованность, живые системы движутся в направлении к своим предпочтительным состояниям, определяемым гомеостатическим равновесием.
Следует, однако, отметить, что анализ конкретных организационных структур при помощи энтропийных критериев не привел к сколько-нибудь интересным результатам. И это, по-видимому, не случайно. Одна из причин заключается в том, что энтропия – слишком общая характеристика системы, не учитывающая специфических особенностей конкретных организационных структур. Имеются и другие причины более принципиального свойства. Одна из них – функциональная природа энтропии. Будучи функциональной характеристикой системы, энтропия, вообще говоря, не затрагивает внутренних структурных особенностей системы, а определяет черты ее поведения в целом. С этой причиной тесно связана вторая – зависимость величины энтропии от наблюдателя. Как уже говорилось, акт наблюдения приводит к понижению энтропии системы за счет превращения ее в информацию. В частности, марковская цепь, находящаяся в равновесии, переводится актом наблюдения в исходное (неравновесное) состояние. При этом энтропия обращается в нуль и мы, казалось бы, должны признать, следуя энтропийным оценкам организованности, что организация системы выросла до максимально возможного значения, хотя с системой как таковой ровным счетом ничего не произошло. По аналогичным соображениям нам пришлось бы признать, что фотография какой-либо статистической системы (например, газового облака) имеет гораздо более высокую организацию, чем сама система. Учитывая, что энтропия системы уменьшается при уменьшении температуры, можно прийти к абсурдному заключению, что труп человека, замерзшего в степи, более организован, чем живой человек.
При приближении к абсолютному нулю всякое вещество, в соответствии с известной теоремой Нернста, приходит в состояние с наименьшей энтропией. Причем энтропия не меняется ни при каких изменениях других термодинамических параметров. Упорядоченность вещества достигает при этом максимальной степени, но сказать то же самое об уровне его организованности, как мы интуитивно себе представляем это понятие, очевидно, нельзя.
Оценка упорядоченности с помощью энтропии также имеет свои особенности. Упорядоченность здесь оценивается лишь в смысле однозначной определенности состояний. Неподвижная груда кирпичей и построенный из кирпичей дом могут оказаться одинаково хорошо упорядоченными с точки зрения энтропийной оценки, поскольку в обоих случаях положение кирпичей фиксировано, однозначно определено.
Действительное значение энтропийные оценки приобретают там, где к системам по тем или иным причинам применяются статистические методы. В этом случае состояние системы, определяемое в терминах, описывающих систему параметров, приобретает известную неопределенность, которая может быть измерена с помощью энтропии. При определенных способах поведения систем эта неопределенность может возрастать или убывать. Максимальная неопределенность достигается в случае, когда все возможные состояния системы становятся равновероятными. Это легко доказывается чисто математически, применением методов оптимизации (например, с помощью метода множителей Лагранжа). С этой точки зрения тепловое равновесие в системах может рассматриваться как термодинамический оптимум по критерию Η; → max. Стремление замкнутых систем перейти в состояние термодинамического оптимума составляет смысл второго начала термодинамики.
Отталкиваясь от термодинамических аналогов, мы привыкли думать, что увеличение энтропии всегда свидетельствует о деградации системы. Можно, однако, привести пример, когда деградация системы сопровождается не увеличением, а уменьшением энтропии. Причем это уменьшение вполне закономерно. Все зависит от того, в каких параметрах определено состояние системы и что мы вкладываем в понятие деградации.
Предположим, что наш объект исследования – это множество людей, проживающих в условиях региональной замкнутости (например, на острове). И допустим, что мы интересуемся распределением населения по возрастам, т.е. хотим знать функцию n (τ), где n – число людей, имеющих возраст τ. Тогда вероятность, что наудачу взятый индивид имеет возраст τ, равна p (τ) = n(τ)/Ν;, где N – общая численность населения острова в некоторый начальный момент времени. Величина неопределенности, которую мы вводим в результате такого статистического подхода, определяется энтропией
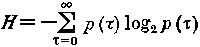
Предположим далее, что по каким-то причинам рождаемость на острове постепенно падает. Тогда численность населения острова будет постепенно убывать, а средний возраст населения постепенно увеличиваться. В конце концов на острове останутся одни старики. Что же произойдет с энтропией? Легко убедиться, что она будет постепенно убывать, в пределе стремясь к нулю. Это уменьшение закономерно, если для падения рождаемости существуют какие-то веские причины.
Если бы вместо параметра "возраст" мы ввели другой параметр (например, "пол"), то получили бы иной аспект исследования, иную статистику. Тогда энтропия определялась бы в терминах вероятности, что наудачу взятый индивид имеет мужской (или женский) пол. Вполне возможно, что в этом случае тоже выполнялся бы закон уменьшения энтропии. Однако падения рождаемости для этого уже недостаточно. Дополнительно необходимо, чтобы средняя продолжительность жизни для разных полов была различной.
Все эти примеры и рассуждения были приведены здесь для того, чтобы показать зависимость энтропийной оценки системы от позиции исследователя, от применяемых исследователем средств, от неопределенности, которая привносится в систему применяемыми средствами. Но если статистический аппарат и прочие понятийные средства определены, то характер изменения энтропии оказывается связанным с реальными процессами, происходящими в системе, и отражает объективные, не зависящие от исследователя факторы.
Посмотрим с этой позиции на старую проблему о соотношении физической энтропии и информации.
Еще в 1929 г. немецкий физик Сциллард, анализируя известный мысленный эксперимент с "демоном Максвелла", показал, что энтропия, теряемая газом за счет разделения молекул на медленные и быстрые, в точности равна информации, получаемой "демоном Максвелла". Другими словами, сумма энтропии и информации в системе "газ- наблюдатель" оказалась постоянной величиной.
Это явилось своего рода сенсацией. В самом деле, здесь мы сталкиваемся с довольно необычной ситуацией. Физическая характеристика становится мерой познания. Причем наблюдатель узнаёт о системе ровно столько, сколько она теряет. Познавая систему, он изменяет ее, "нарушая" при этом второе начало термодинамики. Собственно говоря, такое нарушение действительно неизбежно, поскольку вмешательство наблюдателя, проводящего измерения в системе, нарушает ее замкнутость, а следовательно, исчезают условия, при которых бывает справедлив закон возрастания энтропии.
Можно ли считать, что энтропия действительно способна превращаться в информацию? Некоторые авторы настроены в этом отношении весьма скептически, полагая, что физическая энтропия и энтропия в теории информации имеют лишь формальное и, следовательно, случайное сходство. [6] Другие авторы прямо говорят о том, что энтропия переходит в информацию и что получение наблюдателем какой-либо информации о системе неизбежно приводит к эквивалентному снижению энтропии в этой системе. [7]
Большинство советских философов сходятся на том, что тесная взаимосвязь энтропии и информации не случайна. Вместе с тем сейчас уже не вызывает сомнений, что понятие информации выходит за рамки обычной статистической трактовки и не может быть сведено к энтропии. Его анализ требует более широкого подхода.
Мнение Л. Бриллюэна [8] о том, что энтропия и информация не могут трактоваться порознь и всегда должны рассматриваться совместно, в настоящее время опровергнуто мощным потоком работ по "разнообразностной", семантической и прагматической концепциям информации [9]. Как справедливо отмечает Б. В. Бирюков, статистическая трактовка информации в духе шенноновской теории "положила лишь начало работе по уточнению понятия информации". [10] Это, впрочем, не означает, что анализ глубокой взаимосвязи между энтропией и информацией, проведенный Л. Бриллюэном, лишается смысла. Идея Л. Бриллюэна, пишет Б. В. Бирюков, "имела существенное значение для развития материалистической интерпретации информации (количества информации). Такая интерпретация направлена против спиритуалистских и неопозитивистских интерпретаций феномена информации". [11] Дальнейшее развитие этой интерпретации продолжает оставаться актуальным и сейчас, в особенности если учесть, что дисциплины, в рамках которых строятся надлежащие экспликации анализируемых понятий (в данном случае теория Хартли-Шеннона), существенно помогают, как пишет Б. В. Бирюков, А. Д. Урсул и Г. Н. Поваров [12], философской мысли.
Как бы ни менялись трактовки информации, теорию Хартли-Шеннона отменить нельзя. Так теория относительности Эйнштейна не отменяет механики Ньютона. Было бы опрометчиво спорить с тем, что в явлениях, связанных с превращением энтропии, мы сталкиваемся с феноменом информации. Пусть это лишь одно из проявлений информации, но оно весьма поучительно и многое может прояснить в проблемах, связанных с управлением (в дальнейшем мы надеемся это показать).
Итак, если верно то, что процесс наблюдения приводит к снижению энтропии в статистической системе, то не означает ли это, что энтропия, будучи объективной, физической характеристикой системы, вместе с тем как-то отображает и наш уровень познания системы, задаваемый применяемыми статистическими средствами.
Для того чтобы разобраться в этом вопросе, проанализируем характер использования в данном случае статистических методов. Предположим вначале, что применение функций распределения вероятностей для описания, скажем, идеального газа можно истолковать как нежелание физика следить за положением и скоростью каждой молекулы. (Подобным образом художник отказывается изображать каждый листочек на дереве, стараясь воссоздать на полотне вид кроны в целом.) При таком подходе газ становится локально неопределенной системой. Причем количество этой неопределенности может быть измерено при помощи энтропии. Получается, что энтропия как мера неопределенности системы – это своего рода цена, которую мы заплатили за желание получить лишь целостное представление о системе. Если бы мы провели опыт по измерению координат импульсов всех молекул газа, то полученный объем информации был бы в точности равен энтропии, поскольку неопределенность в этом случае полностью исчезла. Создается видимость, что энтропия газа обусловлена исключительно применением статистических методов. Известная доля истины в этом, безусловно, есть. Имеется, однако, ряд моментов, которые целесообразно в этой связи отметить.
Во-первых, измерение состояний молекул газа в какой-то момент времени не означает, что мы будем знать, где окажутся молекулы в следующую минуту. Неопределенность последующих состояний газа остается. Через несколько соударений молекула вновь погружается в хаос и энтропия системы вырастает до прежнего значения. Другое дело, если бы мы попытались использовать наше знание для целенаправленного вмешательства в систему.
Аналогичная ситуация имеет место и в эксперименте с "демоном Максвелла". Энтропия системы не понизилась бы, если бы "демон" ограничился только измерением, а не производил дополнительную работу по открыванию и закрыванию отверстия, что привело к разделению молекул газа на быстрые и медленные.
Таким образом, сам по себе процесс получения информации о системе путем ее наблюдения не изменяет энтропии системы. Энтропия системы меняется (понижается) только в том случае, если над системой проводится какая-либо целенаправленная работа.
Во-вторых, использование статистических методов не прихоть исследователя. Стохастическое движение частиц газа – по своей природе процесс объективный. Будущие состояния частиц непредсказуемы не потому, что это трудно сделать в силу сложности поведения статистической системы. Они непредсказуемы потому, что в реальных статистических системах не действует принцип лапласовского детерминизма. Дело в том, что в природе не существует абсолютно замкнутых систем. Замкнутость всегда относительна. В механике абстракция замкнутости используется тогда, когда внешними воздействиями на систему по тем или иным причинам можно пренебречь. В статистических системах появляется дополнительная специфика. Отсутствие каких-либо внешних воздействий на систему как целое отнюдь не исключает того, что существует множество локальных взаимодействий с системой (на молекулярном уровне), которые в совокупности компенсируют друг друга и поэтому не приводят к макроскопическому эффекту. Статистическая система может быть замкнутой в макроскопическом смысле, но никогда не бывает изолированной в микроскопическом смысле. Отсюда и непредсказуемость в поведении молекул, а следовательно, неизбежность статистического подхода.
Еще более сложная ситуация складывается в квантовомеханических системах, где невозможно одновременное измерение координат и импульсов в силу соотношения неопределенности Гейзеберга. Неопределенность здесь имеет более глубокую причину, связанную с корпускулярно-волновой природой квантовых объектов. Ограниченность лапласовского детерминизма становится уже теоретическим фактом, и возможности полностью снять неопределенность системы нет при любых средствах наблюдения. Таким образом, энтропийная характеристика статистических систем – это не просто плата за желание ограничиться лишь целостным (функциональным) аспектом рассмотрения. Она возникает с той же степенью необходимости, с какой оказывается здесь необходимым сам функциональный подход. Изъятие энтропии из системы возможно лишь в результате физического воздействия на систему, каким может быть процесс измерения, имеющий целью получить информацию о системе. Но это воздействие с самого начала должно быть устроено таким образом, чтобы соблюдались те особые требования, которые обычно предъявляются к процессу измерения: минимальное возмущающее действие на объект измерения, отсутствие эффектов последействий и т.д. В тех случаях, когда указанные требования не могут быть выполнены (для квантовых объектов это именно так), полученная информация имеет ограниченное значение в том смысле, что не может быть использована для предсказания последующего развития процесса, скажем для определения последующего поведения микрообъекта. Она имеет силу лишь для данного момента, как регистрирующая информация. Поэтому было бы неверно представлять себе дело так, что полученная информация о системе в конце концов снимает всю неопределенность и система перестает быть статистической. Но вполне может оказаться, что накопленная в результате различного рода измерений и экспериментов информация окажется достаточной для того, чтобы построить иные модели процесса, где будет сделан больший акцент на структурные характеристики системы. Построение новой теории потребует новой экспериментальной базы. Изменится цель измерений, изменятся и сами измерительные процедуры. Характер применяемых статистических методов станет иным.
В этих новых условиях мы уже не сможем провести точное количественное сопоставление величины энтропии, как она вычислялась в прежней теории, с приростом объема информации о системе, который был получен в результате эволюции научного знания. Скорее всего такое сопоставление бессмысленно.
Измерение информации требует более широкого подхода и несводимо к вычислению энтропии. Совпадение их в рамках статистической теории говорит о том, что существует нечто общее, что лежит в основе этих понятий. Это общее есть фактор неопределенности. Энтропия как математическая величина дает способ измерить, оценить эту неопределенность при условии, что последняя задается набором альтернатив, каждая из которых имеет определенную вероятность реализации.
Для экспликации понятия количества информации тоже важно уметь измерить неопределенность. Однако способы задания неопределенности могут быть различными. Если она задается набором альтернатив с соответствующими вероятностями, то количество информации может быть измерено с помощью энтропийных оценок. Если же неопределенность задается другим способом, то мера информации соответственно изменяется.
Понятие информации не связано жестко с распределением вероятности в самой системе. Можно представить случай, когда о распределении вероятностей вообще трудно говорить. Тем не менее уместно говорить о получении информации. Например, объект, движущийся по законам классической механики, не является статистической системой и его будущее состояние в принципе полностью предсказуемо. Тем не менее для того, чтобы осуществить такое предсказание, необходимо провести точное измерение координат и импульса движущегося тела, т.е. получить определенную информацию о текущем состоянии системы. Здесь система – источник информации, но понятие физической энтропии к ней не применимо.
Равным образом трудно (хотя и возможно) говорить об энтропии научной книги или художественного произведения, хотя и то и другое – богатые источники информации. Вряд ли кто рискнет заявить, что, читая книгу, он понижает ее энтропию, как это было в эксперименте Сцилларда. Во всяком случае, такое заявление означало бы, что мы попросту отказались понимать энтропию в ее узком, первоначальном, смысле, т.е. в смысле формул Больцмана и Шеннона, и перешли к более широкой трактовке.
Попытки расширительного толкования энтропии имеют место в литературе. Вероятно, этого бы не произошло, не будь совпадения упомянутых формул. И действительно, убедившись однажды в таком совпадении, трудно удержаться от соблазна дальнейших обобщений, особенно если учесть высокую степень актуальности экспликации понятия информации. Заметим, однако, что при расширительной трактовке энтропия, в сущности, перестает быть количественной мерой неопределенности и становится скорее ее синонимом. Учитывая это обстоятельство, было бы, вероятно, целесообразно понимать энтропию лишь в узком смысле, ограничив область ее применения рамками теории вероятности.
В отличие от энтропии информация – общенаучное понятие, приближающееся по своему значению к философской категории. И хотя математическая теория информации К. Шеннона построена на базе теории вероятности, концепция информации существенно выходит за рамки: теории вероятности. Как отмечает А. Н. Колмогоров, "информация по своей природе не специально вероятностное понятие" [13]. В подтверждение этого тезиса А. Н. Колмогоров развивает новый подход к определению количественной меры информации, отталкиваясь от теории алгоритмов [14].
Особенность алгоритмического подхода в теории информации заключается в том, что используемая в нем количественная мера информации предполагает наличие двух множеств. Можно говорить лишь о количестве информации, содержащейся в одном множестве относительно другого. Информация выступает, следовательно, в форме отношения между множествами. Количество ее определяется как минимальная длина программы, однозначно преобразующая одно множество в другое.
На первый взгляд между алгоритмической и энтропийной трактовками информации нет ничего общего. Однако можно провести между ними определенную параллель.
В самом деле, выбор одной альтернативы из некоторого множества возможных предполагает, что в нашем распоряжении имеется алгоритм, который переводит исходное множество альтернатив в множество, содержащее одну альтернативу. Именно по такой схеме осуществляется работа оптимизационных программ. Исходным множеством альтернатив в этом случае является так называемое допустимое множество (область оптимизации). Задача заключается в том, чтобы из допустимого множества выбрать множество оптимальных решений в смысле того или иного критерия. Если программа сложна и содержит большое число, команд (или операций), то можно говорить, следуя А. Н. Колмогорову, что в данном случае оптимум относительно допустимого множества содержит большое количество информации. Вместо этого, впрочем, можно было бы говорить просто о большом количестве информации, переработанной программой.
В рамках энтропийного подхода для оценки количества информации потребовалось бы, во-первых, определение мощности допустимого множества и, во-вторых, определение вероятности того, что элемент из этого множества является оптимальным (для каждого элемента). Если для простоты предположить конечность допустимого множества и равновероятность альтернативных вариантов (за отсутствием других гипотез), то количество информации будет равно логарифму от числа элементов допустимого множества. В какой-то мере это дает представление о сложности алгоритма, в особенности если учесть, что для общего случая дискретной оптимизационной задачи алгоритм решения близок к алгоритму прямого перебора.
В целом же следует признать, что существуют задачи, где алгоритмический подход к информации обладает рядом преимуществ перед энтропийным подходом, во всяком случае в области современных теорий управления, где он хорошо отображает особенности постановок управленческих задач. С общеметодологической точки зрения алгоритмический подход будто бы неплохо согласуется с "разнообразностной" трактовкой информации, развиваемой в работах А. Д. Урсула и Б. В. Бирюкова. Вместе с тем он близок к истолкованию информации как "снятой" неопределенности. Действительно, работу алгоритма можно рассматривать как процесс снятия неопределенности. При этом, как было показано выше, неопределенность может быть представлена множеством альтернатив (допустимым множеством) в виде набора возможных решений. Существование некоторой области возможностей и сама категория возможности играют, по-видимому, важную роль в выяснении природы информации, что делает целесообразным их специальное изучение.
Будем рассматривать неопределенность как некоторое множество возможных исходов. С этой точки зрения неопределенность близка по своему значению к философской категории возможности. Возможность существует в природе объективно. Она не связана с мерой человеческого знания, не обусловлена ограниченностью последнего, а существует самостоятельно как форма присущей природе неоднозначности, потенциального многообразия.
Акт получения информации, снимающий неопределенность, обусловливает проявление одного из возможных исходов в форме действительного факта: возможность превращается в действительность [15].
Представление неопределенности множеством возможных исходов характерно для логико-семантических теорий информации [16]. Однако логико-семантические аспекты информации, сводящиеся к выяснению роли одних высказываний для доказательства истинности (или ложности) других, в сущности, мало затрагивают генетическую природу информации, тесно связанную с феноменом управления. Их задача – определить информационную емкость высказываний. Мы же будем исходить из того, что полученная информация производит определенное воздействие на управляемую систему. Собственно говоря, для этого она только и необходима. Потребляющая информацию система ведет себя по той же схеме, по какой совершается сам акт восприятия информации: если до получения информации существовало множество возможных состояний, дающее представление о потенциальном объеме возможностей системы, то после получения информации будет выбрано одно из этих состояний. Этим состоянием может быть, в частности, то, в котором система находилась (если полученная информация предписывает сохранение состояния).
Снова перед нами акт превращения возможности в действительность. Но теперь этот акт означает преобразование полученной информации в реакцию (движение) системы.
Процессы получения (восприятия) и процессы преобразования информации внутренне связаны и образуют диалектическое единство. Для того чтобы передать (или получить) информацию, необходимо осуществить ее преобразование, при котором одна форма материального движения превращается в другую. Нельзя передать информацию, не преобразовав ее, не придав ей форму, наиболее подходящую для ее распространения в соответствующей физической среде. Так, например, при передаче информации, на большие расстояния удобной формой оказываются электромагнитные колебания. При непосредственном общении людей информационный сигнал воплощается в звуковых колебаниях воздуха. Причем преобразование информации, как правило, носит многоступенчатый характер. Скажем, прежде чем информация станет звуковыми колебаниями, она реализуется в сфере механических колебаний голосовых связок. В свою очередь, колебания голосовых связок вызываются определенной цепью нервных импульсов.
В широком смысле слова поведение системы, выраженное на "языке" ее состояний (или выходных характеристик), тоже может рассматриваться как информационный процесс, как "закодированная" форма управляющей информации. Преобразование информации в поведение системы осуществляется способом, который отвечает структурным особенностям системы, отражает характер закономерностей, описывающих внутренние связи и отношения в системе.
Заслуживает внимания то обстоятельство, что алфавит "поведенческого языка" – набор состояний системы – это вместе с тем и источник неопределенности, дающий некоторое множество возможных альтернатив. В процессе поведения системы каждый раз происходит "снятие" неопределенности в форме перехода возможности в действительность. В каждом таком акте перехода величина "снятой" неопределенности остается одной и той же (поскольку набор возможных состояний фиксирован). Однако в процессе поведения, т.е. при формировании поведенческих "слов" и "фраз", информационное содержание растет по показательному закону.
"Язык движений", по-видимому, имеет большое значение для информационного общения между членами сообществ животных. Н. И. Жуков [17], со ссылкой на работу К. Фриша [18], описывает пример из жизни пчел, когда форма "танца" пчелы-разведчицы информирует рабочих пчел о направлении и примерном расстоянии до места, где расположен источник пищи. Пчелиный танец оказалось возможным выразить математической формулой. Среди рыб и некоторых других видов животных широко используется вибрационный способ сигнализации, особенно характерный для брачного периода.
При определенных условиях информационный процесс, реализуемый поведением системы, выполняет различные другие функции, в частности функции усилителя энергии. Происходит это потому, что при преобразовании информации вовсе не обязательно, чтобы физическая энергия первичного информационного сигнала была равна энергии системы, высвобождающейся при переходе последней в новое состояние. Напомним известный пример, иллюстрирующий эту мысль. Патрон лежит в стволе ружья. Но пуля неподвижна, хотя существует физический закон, по которому газ стремится занять возможно больший объем, а также закон, по которому протекает химическая реакция окисления. Требуется небольшое усилие на спусковой крючок, чтобы создать условия для проявления этих законов. Это небольшое усилие высвобождает большую энергию, во много раз превосходящую энергию начального (пускового) воздействия.
Здесь следует подчеркнуть следующие два момента. Во-первых, существование самой возможности выстрела благодаря тому, что существуют определенные физические законы. Во-вторых, существование определенных условий, при которых физические законы могут проявиться, т.е. перейти из области возможности в область действительности. Роль пускового воздействия заключается в том, что оно формирует необходимые условия для такого перехода. Действуя как мощный усилитель энергии, ружье с информационной точки зрения выступает в роли примитивного "канала связи", по которому передается один бит информации.
Созданный человеком мир техники в значительной степени построен на тех же принципах. Он представляет собой гигантскую систему, усиливающую человеческие возможности в самых различных аспектах деятельности. Используя законы природы, человек производит в ней значительные преобразования, не идущие ни в какое сравнение с теми результатами, которых он мог бы добиться путем непосредственных физических усилий.
Все это имеет немаловажное значение для понимания сущности информационных процессов, позволяет преодолеть устойчивую тенденцию антропоморфного употребления понятия информации, мешающую взглянуть на него как на понятие науки.
"Усилительные функций" информационных воздействий и их роль для понимания природы информации рассмотрены в работе М. И. Сетрова [19]. В частности, автор пишет о том, что пренебрежение физической (в частности, энергетической) стороной дела – характерная черта современных исследований в области теории информации. Предполагается, что реакция системы на информационное воздействие обусловливается "содержанием" сигнала, но никак не его энергией. Между тем, пишет далее М. И. Сетров, "необходимо подчеркнуть, что любое взаимодействие между ними всегда есть только обмен веществом и энергией. Информации как некой самостоятельной сущности, способной наряду с веществом и энергией воздействовать на материальные системы, не существует" [20]. М. И. Сетров склонен рассматривать информацию как особую форму энергетических процессов, когда устанавливается определенное соответствие по силе и сродству энергии сигнала и энергии отображения.
Особенность "энергетического подхода" к определению информации состоит в том, что в нем подчеркивается материальная сторона информационного процесса. С точки зрения этого подхода на вопрос, существует ли информация в природе как нечто, от человека не зависящее, должен быть дан совершенно недвусмысленный ответ: да, существует как особая форма физического взаимодействия в материальных системах. Но "энергетическому подходу", если рассматривать его лишь с этих позиций, присущ и один существенный недостаток: понятие информации теряет "родственные связи" с категорией неопределенности, перестает быть измеримым, как некое особое свойство коммуникативности в системах. Становится недостаточно понятным сам процесс использования информации в управлении. Понимание информации как формы превращения возможности в действительность позволяет преодолеть указанную ограниченность "энергетического подхода", сохранив вместе с тем присущие ему положительные черты.
Информация – это мощный рычаг для преобразования действительности. Механизм использования информации заключается в том, что, опираясь на нее, человек создает определенные условия, при которых законы природы "срабатывают" нужным для него образом. В этом важном обстоятельстве фактически заключена сама природа управления как особого инструмента для превращения возможности в действительность. Оно легло в основу усилителя мыслительных способностей, разработанного Р. Эшби. [21]
Концептуальная основа управления такова. В мире происходит множество различных процессов и движений, но гораздо большее количество движений существует как возможность. Это внутренняя потенция природы, не реализующаяся до тех пор, пока нет всех условий, при которых какое-то из этих движений может осуществиться. С этой точки зрения акт управления – прежде всего процесс формирования условий осуществимости движения. При достижении этих условий все остальное происходит "автоматически", причем таким образом, что полученный результат оказывается соответствующим заранее поставленным целям.
С позиции функционального подхода формирование условий можно мыслить как процесс "приготовления" нужной среды, в которой система будет вести себя нужным образом. Практически речь может идти лишь об отдельных элементах среды, но таких, которые существенно связаны с системой по принципу функциональной замкнутости.
Эти элементы можно структурно присоединить к системе, в результате чего образуется обратная связь и система становится самоуправляемой (см. главу III).
Однако далеко не всегда создание нужной среды – простое дело. Область возможностей, описываемая набором состояний системы, часто оказывается слишком большой для того, чтобы можно было осуществить на этом наборе безошибочный выбор. Такая ситуация характерна для сложных социально-экономических систем, где неопределенность обусловлена наличием большого количества разнообразных факторов. Мы еще недостаточно знаем закономерность проявления этих факторов и не всегда поэтому можем определить последствия принимаемых решений. Существует определенная вероятность получить такие условия, при которых действие социально-экономических законов окажется неожиданным и приведет не к тем результатам, которых мы ожидали. Чтобы уменьшить риск получения отрицательных, неблагоприятных для управляемой экономической системы результатов, разрабатываются математические модели исследуемых экономических ситуаций и с помощью этих моделей осуществляется прогноз последствий от принимаемых решений. Задавая различные значения входящих в модели параметров (что соответствует вариации определенных экономических условий), "проигрывают" на модели возможные траектории поведения системы, исследуют свойства этих траекторий. Получаемая информация хотя и условна, тем не менее дает возможность избежать грубых ошибок, осуществить частичное "снятие" неопределенности. Математические модели позволяют увидеть мир возможных движений, еще не реализованных действительностью, и выбрать среди них те, которые заслуживают реализации с точки зрения стоящих перед нами задач.
Подведем некоторые итоги. В свете сказанного феномен информации предстает перед нами как специфическая форма отражения, обусловливающая переход возможности в действительность в условиях функциональной замкнутости. Специфика информационной формы отражений заключается в том, что в системе отражается не просто состояние среды, рассматриваемой отдельно от системы, а скорее совместный результат взаимодействия системы и среды. В самом "информационном воздействии" важна не величина передаваемой энергии (без которой все-таки немыслимо вообще никакое воздействие), а пространственно-временная структура соответствующего материального носителя энергии. Мир возможностей скрыт за "железными дверями", которые в подавляющем большинстве случаев нельзя открыть ломом, но можно открыть специально подобранным ключом, почти не прилагая усилий. Пространственно-временная структура информационного воздействия как раз и описывает "профиль бородки" упомянутого ключа. Ясно, что он должен быть таков, чтобы открыть нужную дверь, иначе говоря, чтобы возможность, ставшая действительностью, отражала интересы сохранения и дальнейшего развития системы, усиливая (а не ослабляя) тем самым ее единство со средой.
Важность учета неразрывной связи организма и среды, субъекта и объекта для понимания природы информации подчеркивают также А. А. Братко и А. Н. Кочергин. [22] Они указывают на "двойственность" понятия информации, отражающей единство объекта и субъекта и в этом единстве проявляющей свою сущность.
Все это свидетельствует о том, что феномен информации может эффективно использоваться, по-видимому, лишь в рамках функционального подхода. В этом заключается специфика информации как научной категории. [23]
Очерчивая область применимости понятия информации, следует исходить не из расчленения мира на живую и неживую природу, а из того, насколько существенны функциональные аспекты в исследуемой области. Мы знаем, что они существенны в мире живой природы, и не сомневаемся, что там происходят информационные процессы. Функциональные аспекты важны также в сложных кибернетических устройствах (системы автоматического управления, ЭВМ и т.д.). Поэтому и здесь правомерно говорить об информации. Но пожалуй, бесперспективно и нецелесообразно отождествлять информационные процессы с любыми формами отражения, в частности с отражением в мире физических тел, "подведомственном" уже не функциональному, а структурному подходу.
Исключение составляют теория элементарных частиц и современная теория тяготения, где, по-видимому, можно говорить о некоторой специфической форме информационного метаболизма. Основанием для такого суждения являются соображения, изложенные в главе I, о недостаточности традиционного структурного анализа и о роли функциональных аспектов в упомянутых областях знания.
Целенаправленное формирование условий, при которых система в силу своих внутренних, структурных законов начинает функционировать требуемым способом и автоматически достигает при этом нужного результата, есть путь, по которому следует идти, если рассматривать систему как инструмент, орудие для решения тех или иных задач. В данном аспекте рассмотрения система выступает как организация в точном соответствии с тем смыслом, который вкладывался в это понятие первоначально. Слово "организация" происходит от древнегреческого "органон", что означает орудие, инструмент. Позднее с понятием организации стали связывать упорядоченность, закономерное расположение частей в некотором целом. В результате произошло отождествление понятия организации с одним из ее свойств, которое особенно заметно, когда приходится сталкиваться с феноменом организованности. Сущность же организации при этом отходит в тень.
Взяв за основу упорядоченность, закономерность в расположении и взаимосвязи частей внутри целого, мы сразу же попадаем в более широкую область, где на первый план выступает само понятие системы. Теперь между понятием организации и понятием системы устанавливаются настолько тесные отношения, что, по существу, они поглощают друг друга, перестают быть различными. Видимо, не будет большой ошибки рассматривать "всеобщую организационную науку" (тектологию) А. А. Богданова [24] как один из наиболее ранних вариантов общей теории систем, а "общую теорию систем" Л. Берталанфи [25] – как один из более поздних вариантов всеобщей организационной науки.
В. П. Боголепов и А. А. Малиновский указывают, что "сущность организации раскрывается через ее целостность". [26] В свою очередь, целостность, в соответствии с общепринятым мнением, составляет центральный момент в понятии системы.
В работе М. И. Сетрова, [27] предпринявшего попытку последовательного изложения основ организационной теории, системные представления берутся в качестве методологической базы теории. В работе дается обзор основных положений общей теории систем, обсуждается содержание понятия системы. М. И. Сетров рассматривает функциональность как основное свойство организации. Он пишет: "Значимость функционального метода определяется тем, что функциональность есть наиболее существенная сторона любой организации. Поэтому раскрытие законов функционирования и функциональных связей систем и будет раскрытием законов организации". [28] Делая акцент на функциональном подходе, М. И. Сетров тем самым подчеркивает ведущую роль целостности в понятии организации. Следовательно, мы вновь оказываемся в кругу традиционных общесистемных принципов, теряем твердую почву для различения системного исследования и организационной теории.
Конечно, функциональность, целостность сами по себе существенные моменты в понятии организации, которая тоже является системой. Однако, опираясь лишь на системные моменты в понятии организации, мы неизбежно упускаем из виду специфику организационного подхода, которому присущ деятельностный (а не созерцательный) взгляд на систему. Именно деятельностный аспект составляет центральную часть методологий тех исследований, которые проводятся в настоящее время в рамках прикладного системного анализа, ориентированного на проблемы конструирования организации как специального средства для решения проблем.
Вступительная статья С. П. Никанорова к монографии С. Янга [29] дает определенное представление о характере данного направления исследований. В статье, в частности, говорится: "Возникшая в результате распространения идей системного анализа ориентация мышления специалистов на "решение проблем" и "конструирование систем" вполне естественно привела к мысли, что организацию следует рассматривать как совокупность рутинных процессов и процессов решения проблем. В свою очередь совершенствование организации следует рассматривать как улучшение методов, применяемых для выполнения функций решения проблем". [30] Отсюда вытекает, что в основу организационного подхода должны быть положены не исследования и обобщения существующих организационных явлений (хотя это имеет определенное значение как источник накопленного опыта), но прежде всего логическая схема процесса решения проблем и его совершенствования.
Представление об организации как о системе, решающей проблемы, позволяет несколько иначе взглянуть на вопрос об оценке организованности систем, нежели это принято делать на основе понятий энтропии (негэнтропии). О недостатках энтропийного подхода уже говорилось выше. Общий путь решения проблем посредством использования систем состоит, как видим, в том, что подбираются надлежащие параметры среды, при которых система "срабатывает" нужным образом. Подбор среды с надлежащими свойствами является, в свою очередь, проблемой управления. Тот же, кто решает проблему управления, сам представляет собой систему (не обязательно это должен быть человек), выполняющую роль функционального замыкания по отношению к системе-исполнителю. Назовем эту систему управляющей. Присоединение управляющей системы к системе-исполнителю дает систему, обладающую свойством самоорганизации, т.е. систему, способную к самоиспользованию для решения стоящих перед ней проблем.
Представляется естественным связывать уровень организованности системы с понятием сложности задач управления, которые система способна решать. В целом чем более сложные задачи решает система, тем выше уровень ее организованности.
К понятию сложности задач можно подходить с различных точек зрения. Часто здесь применяются сугубо неформальные, субъективные мерки. Если задача плохо формализована, имеет расплывчатую постановку или четко поставлена, но неясно, как ее решать, то человек склонен считать такую задачу сложной. Иногда оказывается, что для четкой формулировки задачи и разработки метода ее решения приходится решать большое количество промежуточных задач. Чем больше таких промежуточных задач, тем более сложной нам представляется исходная задача.
В этих интуитивных представлениях кроется некий объективный смысл. Он легко обнаруживается, если заметить,, что расплывчатость формулировок, отсутствие метода решения суть факторы неопределенности. Для сложных задач неопределенность велика и мы прибегаем к приему декомпозиции. Суть его проста: мы хотим "вычерпать" неопределенность постепенно, мелкими порциями. Точно так же поступают при рытье котлована, уборке помещения, изучении новой дисциплины, прокладывании теплотрасс и т.д.
Таким образом, сложность задачи в конечном итоге определяется размером неопределенности, которую надлежит "снять", т.е. количеством информации, которая перерабатывается в процессе решения задачи. Здесь понятие сложности и понятие количества информации приходят в непосредственное соприкосновение. Оказывается, что для оценки того и другого целесообразно иметь общую меру. Такая мера определяется, в частности, в рамках, уже упомянутого алгоритмического подхода А. Н. Колмогорова. В соответствии с этим подходом сложность задачи управления измеряется минимальной длиной алгоритма (программы), реализующего данную задачу. Даже если мы не всегда умеем построить такой алгоритм, то во всяком случае получаем достаточно прочную методологическую базу для определения уровня организованности систем. Например, можно уверенно сказать, что системы управления перспективным развитием экономики, эксплуатирующие современные оптимизационные методы, более высоко организованы, чем системы, использующие традиционные методы. Внедрение ЭВМ существенно повышает уровень организации экономики. В тех случаях, когда по тем или иным причинам мы не в состоянии определить или хотя бы приблизительно оценить алгоритмическую сложность решаемых задач управления, следует честно признаться, что уровень организованности системы нам не ясен.
Алгоритмический подход к оценке сложности представляется естественным и удобным инструментом для оценки уровня организованности разрабатываемых автоматизированных систем управления. Пожалуй, впервые мы получаем возможность систематически и строго следить за темпами развития организации, количественно сравнивать друг с другом уровни организации отдельных социально-экономических систем – от предприятия до общегосударственной системы хозяйства.
Однако не все задачи управления могут быть формализованы и представлены на языке машинных программ. Примером неформализуемых операций могут служить разработка самих целевых установок в системе, выбор критерия оптимизации. Здесь мы сталкиваемся с проявлением человеческого фактора, со сложностью процессов, протекающих в человеческом мозгу. Оценить сложность в данном случае трудно, так как пока неясна природа алгоритмов, по которым мозг осуществляет свой выбор. Приблизительные оценки можно получить на основе шенноновской меры информации, если отталкиваться от функционального представления системы и вспомнить, что задача управления в общем случае заключается в выборе состояния из некоторого множества Н(А, В). Знание мощности множества Н(А, В) с оценками вероятности для каждого состояния может дать некоторое представление о сложности решаемой задачи, хотя сложность самого отображения Φ : В → Н(А, В) нам неизвестна.
Конечно, данный подход условен хотя бы потому, что никто не знает, какое количество информации приходится перерабатывать для того, чтобы дать оценки вероятностям состояний. Не могут помочь здесь, к сожалению, и иные способы оценки сложности [31], выражаемые в терминах числа отношений на некотором множестве, поскольку в данном случае невозможно провести надлежащую классификацию отношений и даже хоть как-то описать их из-за общей неопределенности рассматриваемой ситуации.
Заметим, что хотя количественную оценку организованности системы в той части, в которой участие человека существенно, нам пока дать не удается, остается еще возможность качественной оценки сложности решаемых управленческих задач (а следовательно, уровня организованности) на основе подхода, развиваемого в главе III. Скачкообразный рост сложности в этом случае может быть объяснен тем, что здесь происходит своего рода "умножение" неопределенностей, описываемых множествами H(А, В) и H(В, H(А, В)).
Не будем вдаваться в тонкости, связанные с проблемой измерения количества информации, которая вполне заслуживает того, чтобы ею заниматься отдельно. Для нас важно другое: принципиальная возможность количественной оценки уровня организованности системы через величину сложности решаемых системой управленческих задач, измеряемую, в свою очередь, количеством информации, перерабатываемой в процессе решения. Организацию, способную решать сложные проблемы, можно считать сложной системой. Но отсюда вовсе не следует, что сложная система непременно должна быть высокоорганизованной. На это обстоятельство указывал, в частности, В. С. Тюхтин [32], который писал, что в общем случае разнообразие и сложность могут иметь как относительно организованный, так и относительно дезорганизованный характер. Данное замечание было сделано В. С. Тюхтиным в порядке возражения против распространенного отождествления понятий сложности и организованности систем, возникающего из энтропийной трактовки явлений сложности.
Рассматривая разнообразие и сложность как основу понятия "количество информации", а организованность как нечто, близкое по смыслу понятию "структурная упорядоченность", В. G. Тюхтин приходит к выводу, что в общем случае количество информации не может служить косвенной оценкой организации систем, а потому информационные оценки не могут служить непосредственными критериями поступательного развития.
Данный вывод носит, пожалуй, излишне обобщающий характер и говорит скорее о том, что традиционное понятие феномена организованности в целом ряде отношений действительно неудовлетворительно. То, что не всякая сложная система является в то же время высокоорганизованной, становится тривиальным фактом, если рассматривать организацию как инструмент для решения проблем, а не просто как структурную упорядоченность. Заметим, кроме того, что в выводе, к которому пришел В. С. Тюх-тин, термин "количество информации" относится к информационному содержанию систем, как заключающему в себе некоторое разнообразие, и не имеет никакого отношения к тому аспекту, в котором он был использован при оценке уровня сложности решаемых задач.
Таким образом, количество информации все-таки может служить косвенной оценкой организации систем, если вложить в это понятие надлежащий смысл, отвечающий упомянутой ранее методологии алгоритмического подхода.
Укажем на важную специфику понятия организации с точки зрения подхода, развиваемого в этом параграфе. Специфика эта заключается в том, что, связывая уровень организованности системы со сложностью решаемых системой задач управления, мы сознательно ограничиваем область применения понятия организации классом систем с ассимилированными обратными связями. Явление организованности выступает как прерогатива кибернетических систем. Оно присуще социальным и биологическим формам движения, а также определенному классу физических и технических систем, где обратная связь играет существенную роль. Но было бы неверно сказать, что организованность присуща облаку пыли, кристаллу, кусочку дерева, хотя все эти предметы, безусловно, обладают определенной структурой и сложностью.
Ограничение понятия организованности классом функционально замкнутых систем позволяет четко определить место и статус теории организации среди других системных дисциплин, создает благоприятные предпосылки для последовательной разработки организационной теории на основе общих систематизирующих принципов и построений дедуктивного характера. Вместе с тем это отвечает практическим интересам сегодняшнего дня, когда проблема построения эффективных организаций приобрела чрезвычайную остроту в связи с непрерывным усложнением общественной и экономической жизни, сопровождаемым в известной степени стихийным и неконтролируемым процессом возникновения и распада различного рода организаций.
Взгляд на организацию как на инструмент достижения целей с самого начала ставит в центр внимания вопросы, связанные с изучением закономерностей процессов принятия решений. Но еще раньше надлежит изучить принципы формирования целей управления, содержательно определить, что такое цель и целеполагание. Будучи имманентным свойством организации, цель как таковая становится важным предметом методологического анализа.